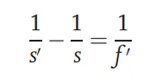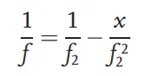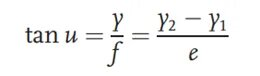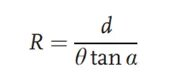1. 광학 시스템의 초점 거리
초점거리는 광학 시스템의 매우 중요한 지표이며, 초점거리의 개념에 대해서는 우리가 어느 정도 이해하고 있으므로 여기서 살펴보겠습니다.
광학 시스템의 초점 거리는 평행광이 입사할 때 광학 시스템의 광학 중심에서 빔의 초점까지의 거리로 정의되며, 광학 시스템에서 빛의 집중 또는 발산을 측정하는 기준입니다. 다음 그림을 통해 이 개념을 설명하겠습니다.
위 그림에서 좌측 끝에서 입사하는 평행 광선은 광학계를 통과한 후 상 초점 F'에 수렴하고, 수렴 광선의 역 연장선은 입사하는 평행 광선의 해당 연장선과 한 점에서 만나고, 이 점을 지나 광축에 수직인 면을 후주평면이라고 하며, 후주평면은 광축과 점 P2에서 만나는데, 이 점을 주점(또는 광학 중심점)이라고 한다. 주점과 상 초점 사이의 거리는 일반적으로 초점거리라고 부르는데, 이 거리의 전체 명칭은 상의 유효 초점거리이다.
그림에서 알 수 있듯이 광학계의 마지막 표면에서 상의 초점 F'까지의 거리를 후초점거리(BFL)라고 합니다. 마찬가지로, 평행광이 오른쪽에서 입사하는 경우에는 유효 초점거리와 전방 초점거리(FFL)라는 개념도 있습니다.
2. 초점 거리 테스트 방법
실제로 광학 시스템의 초점 거리를 시험하는 데 사용할 수 있는 방법은 다양합니다. 초점 거리 시험 방법은 다양한 원리에 따라 세 가지 범주로 나눌 수 있습니다. 첫 번째 범주는 상면의 위치를 기반으로 하고, 두 번째 범주는 배율과 초점 거리의 관계를 이용하여 초점 거리 값을 구하며, 세 번째 범주는 수렴하는 광선의 파면 곡률을 이용하여 초점 거리 값을 구합니다.
이 섹션에서는 광학 시스템의 초점 거리를 테스트하는 데 일반적으로 사용되는 방법을 소개합니다.
2.1C올리메이터 방법
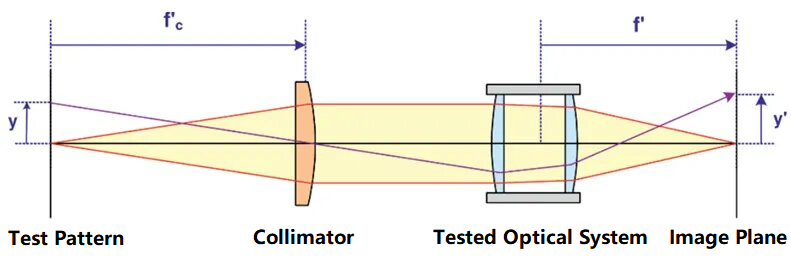
콜리메이터를 사용하여 광학 시스템의 초점거리를 테스트하는 원리는 아래 그림과 같습니다.
그림에서 테스트 패턴은 콜리메이터의 초점에 배치됩니다. 테스트 패턴의 높이 y와 초점 거리 f는c콜리메이터의 '는 알려져 있습니다. 콜리메이터에서 방출된 평행 빔이 테스트 광학 시스템에 의해 수렴되어 이미지 평면에 결상되면, 이미지 평면에서 테스트 패턴의 높이 y'를 기반으로 광학 시스템의 초점 거리를 계산할 수 있습니다. 테스트 광학 시스템의 초점 거리는 다음 공식을 사용할 수 있습니다.
2.2 가우시안M방법
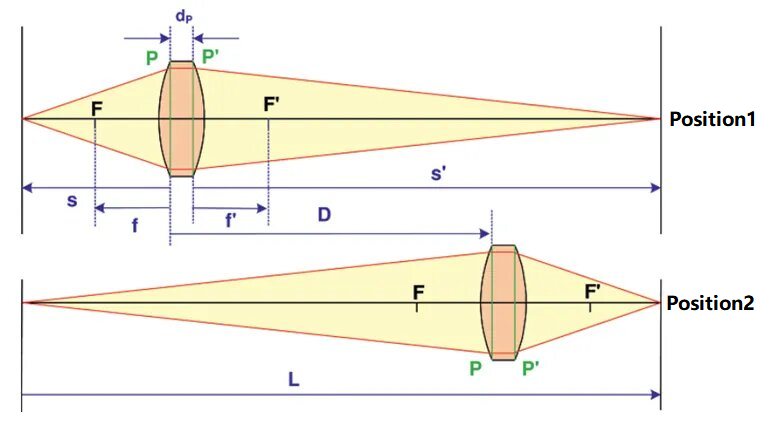
광학 시스템의 초점거리를 테스트하기 위한 가우시안 방법의 개략도는 아래와 같습니다.
그림에서 시험 광학계의 앞면과 뒷면 주평면을 각각 P, P'로 표시하고, 두 주평면 사이의 거리를 d로 표시한다.P. 이 방법에서는 d의 값은P알려진 것으로 간주되거나, 그 값이 작아 무시할 수 있습니다. 물체와 수신 스크린을 왼쪽과 오른쪽 끝에 놓고, 두 물체 사이의 거리를 L로 기록합니다. 여기서 L은 테스트 대상 시스템의 초점 거리의 4배보다 커야 합니다. 테스트 대상 시스템은 각각 위치 1과 위치 2로 표시된 두 위치에 놓일 수 있습니다. 왼쪽 물체는 수신 스크린에 명확하게 나타납니다. 이 두 위치 사이의 거리(D로 표시)를 측정할 수 있습니다. 공액 관계에 따라 다음을 얻을 수 있습니다.
이 두 위치에서 물체 거리는 각각 s1과 s2로 기록되므로 s2 - s1 = D가 됩니다. 공식을 유도하면 아래와 같이 광학 시스템의 초점 거리를 얻을 수 있습니다.
2.3엘엔소미터
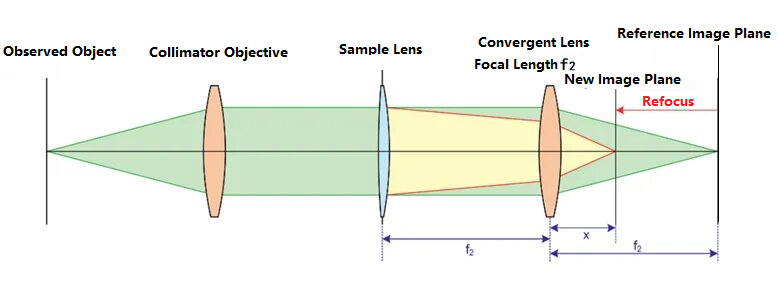
렌소미터는 장초점거리 광학 시스템 시험에 매우 적합합니다. 렌소미터의 개략도는 다음과 같습니다.
첫째, 시험 대상 렌즈는 광 경로에 위치하지 않습니다. 왼쪽의 관측 대상은 콜리메이팅 렌즈를 통과하여 평행광이 됩니다. 평행광은 초점거리 f의 수렴 렌즈에 의해 수렴됩니다.2기준 이미지 평면에 선명한 이미지를 형성합니다. 광 경로가 교정된 후, 피검 렌즈를 광 경로에 배치하고, 피검 렌즈와 수렴 렌즈 사이의 거리를 f로 설정합니다.2결과적으로, 시험 대상 렌즈의 작용으로 인해 광선의 초점이 재조정되어 상면의 위치가 이동하게 되고, 그림에서 새로운 상면의 위치에 선명한 상이 나타납니다. 새로운 상면과 수렴 렌즈 사이의 거리를 x로 표시합니다. 물체-상 관계에 기초하여 시험 대상 렌즈의 초점 거리는 다음과 같이 추론할 수 있습니다.
실제로, 렌즈미터는 안경 렌즈의 상초점 측정에 널리 사용되어 왔으며, 간단한 조작과 신뢰할 수 있는 정밀도라는 장점이 있습니다.
2.4 아베R굴절계
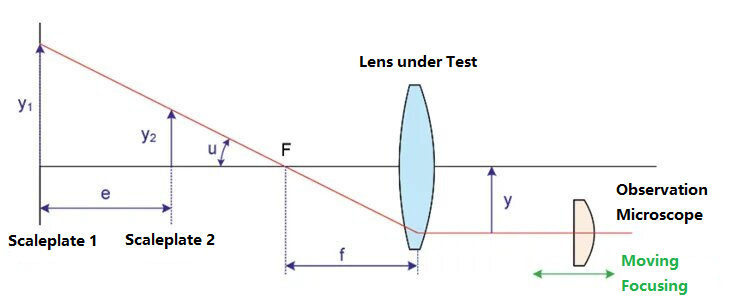
아베 굴절계는 광학계의 초점 거리를 측정하는 또 다른 방법입니다. 개략도는 다음과 같습니다.
시험 렌즈의 물체 표면 쪽에 높이가 다른 두 개의 자, 즉 스케일판 1과 스케일판 2를 놓습니다. 해당 스케일판의 높이는 y1과 y2입니다. 두 스케일판 사이의 거리는 e이고, 자의 윗선과 광축 사이의 각도는 u입니다. 스케일판은 초점 거리가 f인 시험 렌즈에 의해 결상됩니다. 현미경은 상면 끝에 설치됩니다. 현미경의 위치를 이동하여 두 스케일판의 윗면을 찾습니다. 이 때, 현미경과 광축 사이의 거리는 y로 나타냅니다. 물체-상 관계에 따라 초점 거리는 다음과 같습니다.
2.5 모아레 굴절 측정법방법
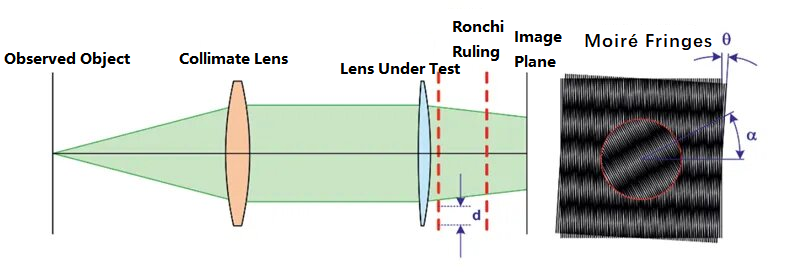
모아레 편향 측정법은 평행 광선에 두 세트의 론키 룰링을 사용합니다. 론키 룰링은 유리 기판에 증착된 격자 모양의 금속 크롬 필름 패턴으로, 광학 시스템의 성능 시험에 일반적으로 사용됩니다. 이 방법은 두 격자에 의해 형성되는 모아레 무늬의 변화를 이용하여 광학 시스템의 초점 거리를 시험합니다. 원리의 개략도는 다음과 같습니다.
위 그림에서, 관찰 대상은 콜리메이터를 통과한 후 평행광이 됩니다. 광 경로에서, 시험 렌즈를 먼저 추가하지 않고 평행광은 변위각 θ와 격자 간격 d를 갖는 두 개의 격자를 통과하여 상면에 모아레 무늬를 형성합니다. 그런 다음, 시험 렌즈를 광 경로에 배치합니다. 원래 콜리메이터에서 굴절된 빛은 특정 초점 거리를 생성합니다. 광선의 곡률 반경은 다음 공식으로 구할 수 있습니다.
일반적으로 테스트 대상 렌즈는 첫 번째 회절격자에 매우 가깝게 배치되므로, 위 공식의 R 값은 렌즈의 초점거리에 해당합니다. 이 방법의 장점은 양의 초점거리 시스템과 음의 초점거리 시스템의 초점거리를 테스트할 수 있다는 것입니다.
2.6 광학F이베르A자동 시준M방법
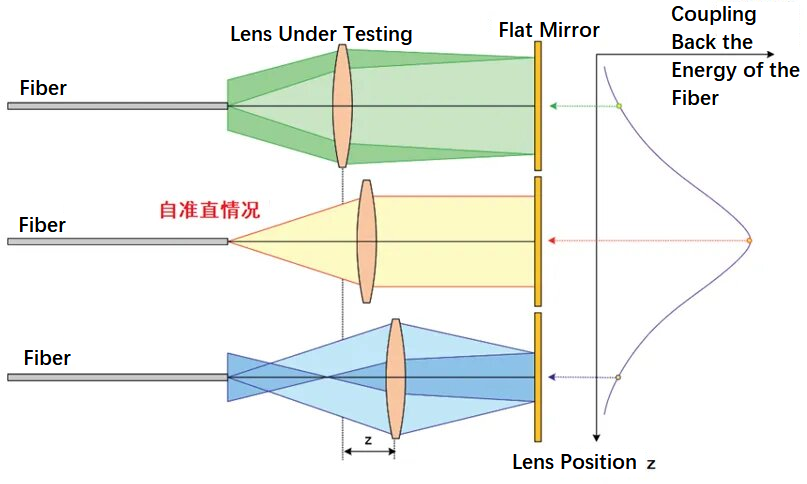
렌즈의 초점 거리를 시험하기 위해 광섬유 자동 시준법을 사용하는 원리는 아래 그림과 같습니다. 광섬유를 사용하여 시험 대상 렌즈를 통과한 발산 빔을 평면 거울에 조사합니다. 그림에서 세 가지 광학 경로는 각각 초점 내, 초점 내, 초점 외 광섬유의 상태를 나타냅니다. 시험 대상 렌즈의 위치를 앞뒤로 이동시키면 초점에서 광섬유 헤드의 위치를 찾을 수 있습니다. 이때 빔은 자체 시준되고, 평면 거울에서 반사된 후 대부분의 에너지는 광섬유 헤드 위치로 되돌아옵니다. 이 방법은 원리가 간단하고 구현이 쉽습니다.
3. 결론
초점거리는 광학 시스템의 중요한 매개변수입니다. 본 논문에서는 광학 시스템 초점거리의 개념과 그 시험 방법을 자세히 설명합니다. 모식도와 함께 상측 초점거리, 물체측 초점거리, 전후 초점거리의 개념을 포함한 초점거리의 정의를 설명합니다. 실제로 광학 시스템의 초점거리를 시험하는 방법은 다양합니다. 본 논문에서는 콜리메이터법, 가우시안법, 초점거리 측정법, 아베 초점거리 측정법, 모아레 편향법, 광섬유 자동 콜리메이션법의 시험 원리를 소개합니다. 본 논문을 읽으시면 광학 시스템의 초점거리 매개변수에 대한 이해가 깊어지실 것으로 믿습니다.
게시 시간: 2024년 8월 9일